Delaunay/Voronoi intersected with boundary
|
Hello,
I have the following problem: I have a number of particles within a certain boundary shape (the cell). I am interested in measuring the average distance of a particle to its neighbours. A neighbor would be defined by the Voronoi diagramm as particles with a common edge in the Voronio map. I am aware that the Delaunay triangulation can gives me precisely that, but there is one problem: It doesn't take into account the boundary of the domain. I.e. two particles will be considered neighbors, even if their Voronoi domains intersect OUTSIDE of the full domain (the cell). Does anyone have an idea to avoid this? Thank you and many regards, Angelika |
Re: Delaunay/Voronoi intersected with boundary
|
I’d have to see diagrams to see if the cases are similar, but in analogous cases I restrict analysis to Voronoi regions whose vertices are INSIDE the bounding area.
In most Voronoi analysis, it is wise to eliminate a border region. The precise method for doing this depends on the problem. -- Kenneth Sloan [hidden email] Vision is the art of seeing what is invisible to others. > On Apr 28, 2016, at 16:06 , schiriki <[hidden email]> wrote: > > Hello, > > I have the following problem: I have a number of particles within a certain > boundary shape (the cell). I am interested in measuring the average distance > of a particle to its neighbours. A neighbor would be defined by the Voronoi > diagramm as particles with a common edge in the Voronio map. > > I am aware that the Delaunay triangulation can gives me precisely that, but > there is one problem: It doesn't take into account the boundary of the > domain. I.e. two particles will be considered neighbors, even if their > Voronoi domains intersect OUTSIDE of the full domain (the cell). > > Does anyone have an idea to avoid this? > > Thank you and many regards, > Angelika > > > > > > -- > View this message in context: http://imagej.1557.x6.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272.html > Sent from the ImageJ mailing list archive at Nabble.com. > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
Re: Delaunay/Voronoi intersected with boundary
|
In reply to this post by schiriki
The Voronoi gives distances to some of the nearest neighbors - there can be neighboring particles closer than some of particles that are identified by the Voronoi that are excluded because there is a closer particle in that direction. The Voronoi is really about dividing up an area based on proximity to the nearest object not assessing nearest neighbors.
If you really want the average distance to a given number of neighbors you could to trawl through a list of coordinates - which can get slow if the numbers are very large. Edges are definitely a problem and of course you need to work with a 3D dataset as 2D distances may not reflect the 3D. Edge effects can be eliminated by also examining the volume around each object - a distance transform that is then masked by the volume of the cell will work. If you then multiply the binary image showing all objects with the DT around one particle, the histogram of this image gives the distance of every object from your source object. So you can get the profile of the volume around a single object and a profile of the number of objects around your chosen object - compare the two. Repeat for many objects. It is also good idea to compare the distribution you have with a randomized distribution. ________________________________________ From: ImageJ Interest Group [[hidden email]] on behalf of schiriki [[hidden email]] Sent: 28 April 2016 23:06 To: [hidden email] Subject: Delaunay/Voronoi intersected with boundary Hello, I have the following problem: I have a number of particles within a certain boundary shape (the cell). I am interested in measuring the average distance of a particle to its neighbours. A neighbor would be defined by the Voronoi diagramm as particles with a common edge in the Voronio map. I am aware that the Delaunay triangulation can gives me precisely that, but there is one problem: It doesn't take into account the boundary of the domain. I.e. two particles will be considered neighbors, even if their Voronoi domains intersect OUTSIDE of the full domain (the cell). Does anyone have an idea to avoid this? Thank you and many regards, Angelika -- View this message in context: http://imagej.1557.x6.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272.html Sent from the ImageJ mailing list archive at Nabble.com. -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
In reply to this post by Kenneth Sloan-2
Hello Kenneth,
thank you for your help. I attached an image to better explain the problem. Since in my datasets all or almost all particles will be near the domain border, the problem arises a lot. The picture shows the particles, the domain boundary (close to a rectangle) and the Voronio as computed by imageJ. If I want to use Delaunay to determine distances, also e.g. the particles marked with red or those marked with blue will be considered neighbors, eventhough their Voronoi domains do not share an edge inside the domain. 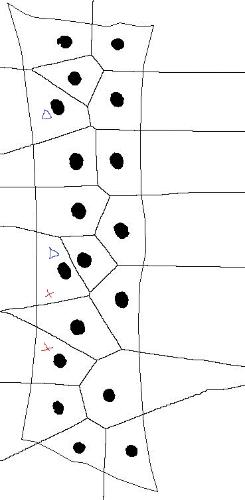 For a single image I could maybe mirror the particles along the border to enforce real Voronoi separation, but I have a lot of data, so doing it by hand is not an option. Thank you, Angelika |
Re: Delaunay/Voronoi intersected with boundary
|
Hi Angelika,
if you don't need it too accurate, you can try with the simple ImageJ Voronoi approximation. Smething like this: //convert to single points by 'Find Maxima', //unless you are interested in the distance between the outlines run("Find Maxima...", "noise=0 output=[Single Points] light"); run("Voronoi"); setThreshold(0, 0); run("Create Selection"); run("Set...", "value=255"); run("Select None"); run("Grays"); //makes sure we have a non-inverting LUT run("Find Maxima...", "noise=2 output=[Single Points] exclude light"); run("Create Selection"); run("Select None"); //gets selection into undo buffer close(); run("Restore Selection"); //transfer selection to Voronoi image run("Histogram"); The histogram will roughly be the distance distribution in units of twice the pixel size. Michael ________________________________________________________________ On 2016-04-29 17:13, schiriki wrote: > Hello Kenneth, > > thank you for your help. I attached an image to better explain the problem. > Since in my datasets all or almost all particles will be near the domain > border, the problem arises a lot. > The picture shows the particles, the domain boundary (close to a rectangle) > and the Voronio as computed by imageJ. If I want to use Delaunay to > determine distances, also e.g. the particles marked with red or those marked > with blue will be considered neighbors, eventhough their Voronoi domains do > not share an edge inside the domain. > > <http://imagej.1557.x6.nabble.com/file/n5016282/example.jpg> > > For a single image I could maybe mirror the particles along the border to > enforce real Voronoi separation, but I have a lot of data, so doing it by > hand is not an option. > > Thank you, > Angelika > > > > -- > View this message in context: http://imagej.1557.x6.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272p5016282.html > Sent from the ImageJ mailing list archive at Nabble.com. > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html > -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
Re: Delaunay/Voronoi intersected with boundary
|
In reply to this post by schiriki
That’s a difficult case. My first thought is to use only Voronoi edges with at least one vertex inside the boundary. I think that’s actually what you initially proposed. If the entire boundary between Voronoi edges is outside the boundary, those two particles are not really neighbors.
As someone else noted (sorry - I don’t have the posting handy), Voronoi may not be giving exactly what you want here. It depends on the interpretation of the particles and the Voronoi domains. I might, for example, look at the line segment connecting two of your particles, and exclude those which do not strictly intersect the Voronoi edge separating the corresponding domains. This is just a crude heuristic, but I think it addresses the question of what you really mean by saying that isolated particles are “neighbors”. for example, in your image, look at the right hand column of particles. Counting up from the bottom, the 2nd and 3rd particles are Voronoi neighbors, but I think it’s defensible to call them “NOT neighbors” for the purpose of your analysis. Similarly, looking at the left hand column of particles, near the top, the 1st and 2rd particles on the left don’t really qualify as “neighbors”. There are a couple of other examples I think. I like this heuristic. For each Voronoi edge, generate the dual Delaunay edge. If the two edges intersect properly, call the particles neighbors and use the length of the Delaunay edge in further computation. If not, not. — Kenneth Sloan [hidden email] Vision is the art of seeing what is invisible to others. > On Apr 29, 2016, at 11:13 , schiriki <[hidden email]> wrote: > > Hello Kenneth, > > thank you for your help. I attached an image to better explain the problem. > Since in my datasets all or almost all particles will be near the domain > border, the problem arises a lot. > The picture shows the particles, the domain boundary (close to a rectangle) > and the Voronio as computed by imageJ. If I want to use Delaunay to > determine distances, also e.g. the particles marked with red or those marked > with blue will be considered neighbors, eventhough their Voronoi domains do > not share an edge inside the domain. > > <http://imagej.1557.x6.nabble.com/file/n5016282/example.jpg> > > For a single image I could maybe mirror the particles along the border to > enforce real Voronoi separation, but I have a lot of data, so doing it by > hand is not an option. > > Thank you, > Angelika > > > > -- > View this message in context: http://imagej.1557.x6.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272p5016282.html > Sent from the ImageJ mailing list archive at Nabble.com. > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
Re: Delaunay/Voronoi intersected with boundary
|
Following up - has anyone encountered this concept of filtering Voronoi neighbors by the criterion that the Voronoi-edge and it’s dual Delaunay-edge strictly intersect?
If so, please educate me with a citation If not, I’ll claim it. [sadly, I often “invent” things that I have seen previously, and then “forgotten” - they say that memory is the second thing to go as you age] -- Kenneth Sloan [hidden email] Vision is the art of seeing what is invisible to others. > On Apr 29, 2016, at 15:28 , Kenneth Sloan <[hidden email]> wrote: > > That’s a difficult case. My first thought is to use only Voronoi edges with at least one vertex inside the boundary. I think that’s actually what you initially proposed. If the entire boundary between Voronoi edges is outside the boundary, those two particles are not really neighbors. > > As someone else noted (sorry - I don’t have the posting handy), Voronoi may not be giving exactly what you want here. It depends on the interpretation of the particles and the Voronoi domains. I might, for example, look at the line segment connecting two of your particles, and exclude those which do not strictly intersect the Voronoi edge separating the corresponding domains. This is just a crude heuristic, but I think it addresses the question of what you really mean by saying that isolated particles are “neighbors”. > > for example, in your image, look at the right hand column of particles. Counting up from the bottom, the 2nd and 3rd particles are Voronoi neighbors, but I think it’s defensible to call them “NOT neighbors” for the purpose of your analysis. > > Similarly, looking at the left hand column of particles, near the top, the 1st and 2rd particles on the left don’t really qualify as “neighbors”. There are a couple of other examples I think. > > I like this heuristic. For each Voronoi edge, generate the dual Delaunay edge. If the two edges intersect properly, call the particles neighbors and use the length of the Delaunay edge in further computation. If not, not. > > — > Kenneth Sloan > [hidden email] > Vision is the art of seeing what is invisible to others. > > > > >> On Apr 29, 2016, at 11:13 , schiriki <[hidden email]> wrote: >> >> Hello Kenneth, >> >> thank you for your help. I attached an image to better explain the problem. >> Since in my datasets all or almost all particles will be near the domain >> border, the problem arises a lot. >> The picture shows the particles, the domain boundary (close to a rectangle) >> and the Voronio as computed by imageJ. If I want to use Delaunay to >> determine distances, also e.g. the particles marked with red or those marked >> with blue will be considered neighbors, eventhough their Voronoi domains do >> not share an edge inside the domain. >> >> <http://imagej.1557.x6.nabble.com/file/n5016282/example.jpg> >> >> For a single image I could maybe mirror the particles along the border to >> enforce real Voronoi separation, but I have a lot of data, so doing it by >> hand is not an option. >> >> Thank you, >> Angelika >> >> >> >> -- >> View this message in context: http://imagej.1557.x6.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272p5016282.html >> Sent from the ImageJ mailing list archive at Nabble.com. >> >> -- >> ImageJ mailing list: http://imagej.nih.gov/ij/list.html > -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
In reply to this post by Michael Schmid
Hi Michael,
thank you for your help. I admit, I don't really understand your suggestion, probably because I am not familiar enough with imageJ. In what way does your protocol take care of the domain boundary? Thank you and many regards, Angelika |
|
In reply to this post by Kenneth Sloan-2
Hi Kenneth,
I see what you mean and I agree that there are some cases where "neighbor" might not be the right word. However, in my particular case the Voronoi diagramm is not just a way to define neighbors, but it has a biological meaning, i.e. it defines the sections for which each particle is "responsible". That is why I would like to stick to the "definition" of neighbor, where I am your neighbor if our "responsibility areas" have a common edge. Therefore any solution would really have to use the boundary data. But if I come across another problem where your "neighbor"-definition fits, I'll keep it in mind! Many thanks for the help, Angelika |
Re: Delaunay/Voronoi intersected with boundary
|
In reply to this post by Kenneth Sloan-2
On Friday 29 Apr 2016 15:40:32 Kenneth Sloan wrote:
> Following up - has anyone encountered this concept of filtering Voronoi > neighbors by the criterion that the Voronoi-edge and it’s dual > Delaunay-edge strictly intersect? > > If so, please educate me with a citation > > If not, I’ll claim it. Interesting question. The graph joining those points has to be a subgraph of the Delaunay graph, of course. I wonder if you get a very similar result to the Gabriel Graph? https://en.wikipedia.org/wiki/Gabriel_graph Cheers Gabriel (not that one) :-) -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
Re: Delaunay/Voronoi intersected with boundary
|
Don’t know. I’ll add this to my stack (sadly, not a queue) of things to investigate.
My current thought is: yes - the results will be similar, and might be identical. -- Kenneth Sloan [hidden email] Vision is the art of seeing what is invisible to others. > On Apr 30, 2016, at 11:09 , Gabriel Landini <[hidden email]> wrote: > > On Friday 29 Apr 2016 15:40:32 Kenneth Sloan wrote: >> Following up - has anyone encountered this concept of filtering Voronoi >> neighbors by the criterion that the Voronoi-edge and it’s dual >> Delaunay-edge strictly intersect? >> >> If so, please educate me with a citation >> >> If not, I’ll claim it. > > Interesting question. > The graph joining those points has to be a subgraph of the Delaunay graph, of > course. I wonder if you get a very similar result to the Gabriel Graph? > > https://en.wikipedia.org/wiki/Gabriel_graph > > Cheers > > Gabriel (not that one) :-) > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
Hi!
Thank you Gabriel for the input. I'll definitely have a look into the Gabriel graph. In the meanwhile I found a solution that is not perfect, but works for me at the moment: 1. Since my cells are almost rectangles, I approximate the boundary by a bounding rectangle around the particles 2. I mirror all points along the rectangles edges (it's a bit of an overkill, would probably be enough to mirror along the nearest edge) 3. I calculate the Delaunay triangulation 4. I filter the segments that actually connect the original points (i.e. the ones inside the rectangle) 5. I take the averages the get the mean distance to neighbors defines by the Voronoi Comments: - Assuming an rectangular domain, by this procedure I enforce Voronoi edges along the rectangle without changing the Voronoi inside the rectangle (one would have to proof this) - I attached two pictures 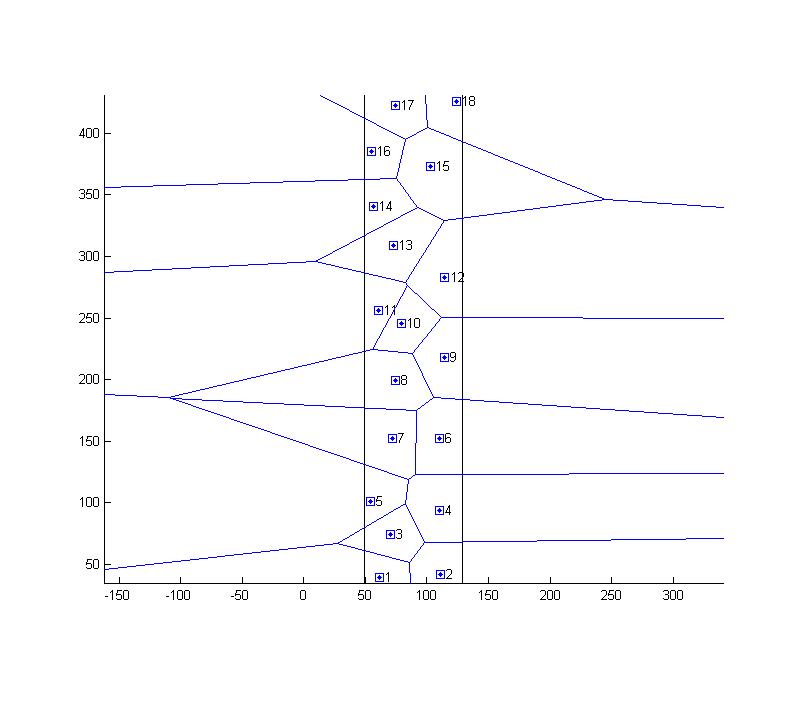 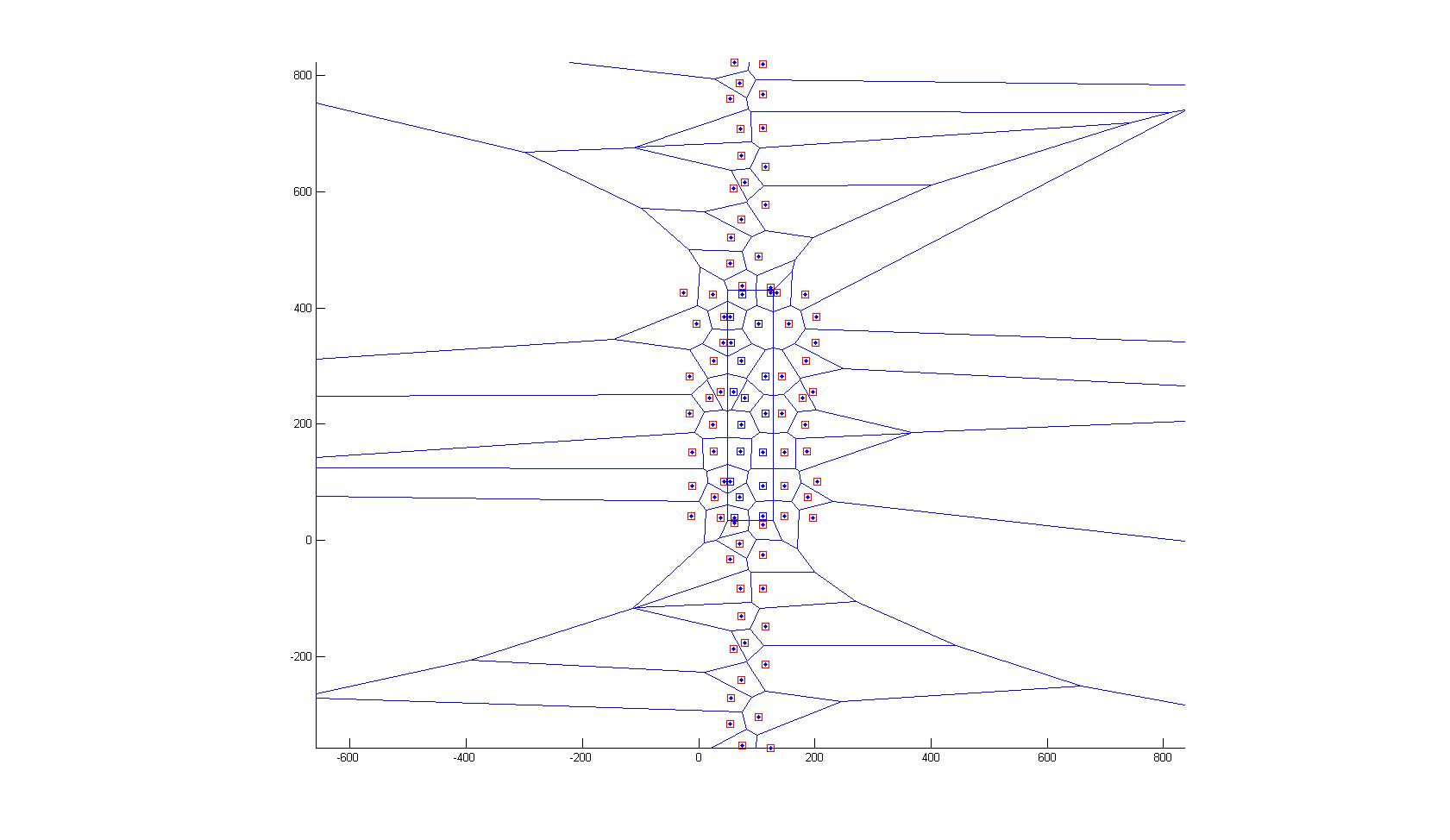 Due to my lack of imageJ programing skills I implemented in in Matlab. If I come up with a better solution (and I am sure it exists), I'll post it. Many regards, Angelika |
Re: Delaunay/Voronoi intersected with boundary
|
Hi all,
I implemented a version of this Gabriel Graph in case anyone is interested https://github.com/lacan/ijp-gabriel-graph You can grab the jar from the 'target' folder. Note that you'll need Java 8 to run this as it's making use of a few features from the Collection class. All the best Oli -----Original Message----- From: ImageJ Interest Group [mailto:[hidden email]] On Behalf Of schiriki Sent: lundi, 2 mai 2016 16:27 To: [hidden email] Subject: Re: Delaunay/Voronoi intersected with boundary Hi! Thank you Gabriel for the input. I'll definitely have a look into the Gabriel graph. In the meanwhile I found a solution that is not perfect, but works for me at the moment: 1. Since my cells are almost rectangles, I approximate the boundary by a bounding rectangle around the particles 2. I mirror all points along the rectangles edges (it's a bit of an overkill, would probably be enough to mirror along the nearest edge) 3. I calculate the Delaunay triangulation 4. I filter the segments that actually connect the original points (i.e. the ones inside the rectangle) 5. I take the averages the get the mean distance to neighbors defines by the Voronoi Comments: - Assuming an rectangular domain, by this procedure I enforce Voronoi edges along the rectangle without changing the Voronoi inside the rectangle (one would have to proof this) - I attached two pictures <http://imagej.1557.x6.nabble.com/file/n5016297/Voronoi.jpg> <http://imagej.1557.x6.nabble.com/file/n5016297/extendedVoronoi.jpg> Due to my lack of imageJ programing skills I implemented in in Matlab. If I come up with a better solution (and I am sure it exists), I'll post it. Many regards, Angelika -- View this message in context: http://imagej.1557.x6.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272p5016297.html Sent from the ImageJ mailing list archive at Nabble.com. -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
«
Return to ImageJ
|
1 view|%1 views
| Free forum by Nabble | Edit this page |

