Macro code to fit a spline to two segments
|
This post was updated on .
Hi there,
I need to calculate the length of a spline fitted to two straight lines and I am trying to write a macro for this. The attached figure illustrates the situation. I went as far as to calculate segments AB and BC, and angles alpha and beta. the distance "d" is known. What should I do next? try to get the coordinates of A, B and C? And then what? Some suggesting of macro scripts or directions would be much appreciated! 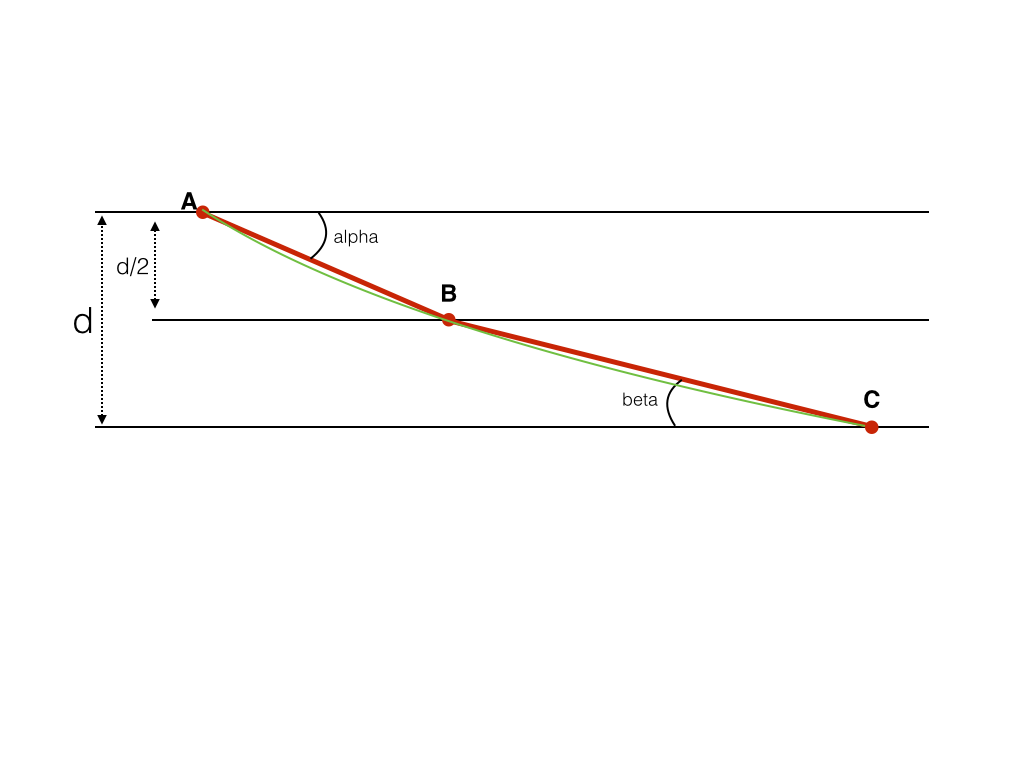 EDIT: I changed the title to reflect more precisely what I need help with |
|
Hi Oliver,
On Aug 8, 2014, at 8:12 AM, olivier <[hidden email]> wrote: > Hi there, > > I need to calculate the length of a spline fitted to two straight lines and > I am trying to write a macro for this. > The attached figure illustrates the situation. > > I went as far as to calculate segments AB and BC, and angles alpha and beta. > the distance "d" is known. > > What should I do next? try to get the coordinates of A, B and C? And then > what? Some suggesting of macro scripts or directions would be much > appreciated! > > <http://imagej.1557.x6.nabble.com/file/n5009069/geometry.png> > I am not 100% sure I understand what you are after. It appears to me that you know segments AB and BC, and, therefore, you have an estimate of the length of the spline. Don't you? Cheers, Ben > > > -- > View this message in context: http://imagej.1557.x6.nabble.com/geometric-challenge-tp5009069.html > Sent from the ImageJ mailing list archive at Nabble.com. > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
Thanks for your reply Ben. What I would like help with is to write the macro code to fit a spline to these segments and get the length of the spline...
|
|
Dear Olivier, yes indeed if you vave the image coordinates ofA B and C you have :
AB^2 = (xB-xA)^2+(yB-yA)^2 also: AB^2 = (xB-xA)^2+(d/2)^2 the same for BC^2 = (xC-xB)^2+(yC-yB)^2 BC^2 = (xC-xB)^2+(d/2)^2 For angle : d/2 = AB*sin(alpha) alpha = arcsin(d/2 / AB) beta = arcsin(d/2 / BC) Hope it helps... Leon Le 25 août 2014 à 21:12, olivier a écrit : > Anyone? > > > > -- > View this message in context: http://imagej.1557.x6.nabble.com/Macro-code-to-fit-a-spline-to-two-segments-tp5009069p5009338.html > Sent from the ImageJ mailing list archive at Nabble.com. > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
On Tuesday 26 Aug 2014 09:14:09 Leon Espinosa wrote:
> Dear Olivier, yes indeed if you vave the image coordinates ofA B and C you > have : > > AB^2 = (xB-xA)^2+(yB-yA)^2 > also: [...] I think Olivier wants the spline length (in green) not the polyline (in red). I do not think that one can obtain this analytically unless you know what type of spline it is (i.e. what is the function used to generate the green line). Once you know the function perhaps you can use calculus to find the function length. http://en.wikipedia.org/wiki/Arc_length If you try to measure the chain of pixels forming the green line you will get an overestimation of the length as the curves on screen are constructed in steps of 1 or sqrt(2). (By the way, this is the reason why we do not get 1.0 as Circularity of a discrete circle; the perimeter estimation ends up longer than it is for a perfect circle). By using a spline interpolation, you are making already assumptions about the points being appropriately fitted by such spline and that the original data is differentiable (for example at a higher magnification the spline might not fit the data at all; think of a fractal curve). Unless you know that those assumptions are correct, perhaps Leon's approach (estimating the length of the polyline) at a particular resolution might be better (and specify the resolution when you report the length). Cheers Gabriel -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
Dear Olivier,
You could create the ABC polyline, fit a spline to it and measure its length: open("http://imagej.1557.x6.nabble.com/file/n5009069/geometry.png"); makeLine(203,212,449,320,872,427); run("Properties... ", "stroke=cyan"); roiManager('add'); run("Fit Spline"); run("Properties... ", "stroke=blue"); roiManager('add'); List.setMeasurements; length = List.getValue('Length'); print (length); setOption('show all', true); Jerome. On 26 August 2014 12:01, Gabriel Landini <[hidden email]> wrote: > On Tuesday 26 Aug 2014 09:14:09 Leon Espinosa wrote: > > Dear Olivier, yes indeed if you vave the image coordinates ofA B and C > you > > have : > > > > AB^2 = (xB-xA)^2+(yB-yA)^2 > > also: > [...] > I think Olivier wants the spline length (in green) not the polyline (in > red). > > I do not think that one can obtain this analytically unless you know what > type > of spline it is (i.e. what is the function used to generate the green > line). > Once you know the function perhaps you can use calculus to find the > function > length. > http://en.wikipedia.org/wiki/Arc_length > > If you try to measure the chain of pixels forming the green line you will > get > an overestimation of the length as the curves on screen are constructed in > steps of 1 or sqrt(2). (By the way, this is the reason why we do not get > 1.0 > as Circularity of a discrete circle; the perimeter estimation ends up > longer > than it is for a perfect circle). > > By using a spline interpolation, you are making already assumptions about > the points being appropriately fitted by such spline and that the original > data is differentiable (for example at a higher magnification the spline > might > not fit the data at all; think of a fractal curve). Unless you know that > those > assumptions are correct, perhaps Leon's approach (estimating the length of > the > polyline) at a particular resolution might be better (and specify the > resolution when you report the length). > > Cheers > > Gabriel > > -- > ImageJ mailing list: http://imagej.nih.gov/ij/list.html > -- Jerome Mutterer CNRS - Institut de biologie moléculaire des plantes 12, rue du Général Zimmer 67084 Strasbourg Cedex T 0367155339 www.ibmp.cnrs.fr -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
Hi Jerome,
On Tuesday 26 Aug 2014 13:48:36 Jerome Mutterer wrote: > You could create the ABC polyline, fit a spline to it and measure its > length: [...] Nice one, more brains think better than one :-) The straight line is 704.987 pixels which is correct, but the curved 705.450. Is that correct, less than half pixel longer? Cheers Gabriel -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
Re: geometric challenge :)
|
On Aug 26, 2014, at 8:43 AM, Gabriel Landini wrote:
> Hi Jerome, > > On Tuesday 26 Aug 2014 13:48:36 Jerome Mutterer wrote: >> You could create the ABC polyline, fit a spline to it and measure its >> length: > [...] > > Nice one, more brains think better than one :-) > The straight line is 704.987 pixels which is correct, but the curved 705.450. > Is that correct, less than half pixel longer? Hard to believe but the following macro, which calculates the line length by summing the lengths of the segments, reports the same lengths as the Measure command. There are 3 segments in the base line and 352 in the spline fitted version. -wayne newImage("Untitled", "8-bit black", 900, 500, 1); makeLine(203,212,449,320,872,427); printLength(); Overlay.addSelection("cyan"); makeLine(203,212,449,320,872,427); run("Fit Spline"); printLength(); Overlay.addSelection("magenta"); function printLength() { List.setMeasurements; len1 = List.getValue('Length'); getSelectionCoordinates(x, y); len2 = 0; for (i=0; i<x.length-1; i++) { dx = x[i+1] - x[i]; dy = y[i+1] - y[i]; d = sqrt(dx*dx+dy*dy); len2 += d; } print(len1, len2, x.length); } -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
On Tuesday 26 Aug 2014 16:50:48 Rasband, Wayne [E] wrote:
> Hard to believe but the following macro, which calculates the line length by > summing the lengths of the segments, reports the same lengths as the > Measure command. There are 3 segments in the base line and 352 in the > spline fitted version. [...] Thanks Wayne. Yes, this is counter-intuitive. I tried drawing the selection and the fitted splines and measure the length of the chain of pixels using Lines8 (which overestimates lengths as it measures from pixel to pixel). I get the same length for both curves: 758.056. Also interesting is that both curves have exactly the same number of pixels (670). I suppose that this is due to the approximation of the curve with segments? The analytical solution to the length of the spline and the length of the segments determined by the 3 points cannot be the same. Cheers Gabriel -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
|
Thanks to all for your help!
|
|
In reply to this post by Rasband, Wayne (NIH/NIMH) [E]
Just as a follow up in case there is further interest.
These papers discuss the issues encountered when computing lengths and perimeters in discrete blobs: Kulpa, Z. Area and perimeter measurement of blobs indiscrete binary pictures. Computer Graphics and Image processing 6:434-451, 1977. Ellis & Proffitt . Measurement of the lengths of digitised curved line Computer Graphics and Image processing 10:333-347, 1979. Kulpa Z. More about areas and perimeters of quantized objects. Computer Vision, Graphics, and Image Processing, Volume 22, Issue 2, May 1983, Pages 268-276 Yang et al. Methods to estimate areas and perimeters of blob-like objects: a comparison. In Proc. IAPR Workshop on Machine Vision Applications, pp.272276 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.143.4018 Cheers Gabriel -- ImageJ mailing list: http://imagej.nih.gov/ij/list.html |
«
Return to ImageJ
|
1 view|%1 views
| Free forum by Nabble | Edit this page |


