Re: Delaunay/Voronoi intersected with boundary

Posted by schiriki on
URL: http://imagej.273.s1.nabble.com/Delaunay-Voronoi-intersected-with-boundary-tp5016272p5016297.html

Hi!

Thank you Gabriel for the input. I'll definitely have a look into the Gabriel graph. In the meanwhile I found a solution that is not perfect, but works for me at the moment:
1. Since my cells are almost rectangles, I approximate the boundary by a bounding rectangle around the particles
2. I mirror all points along the rectangles edges (it's a bit of an overkill, would probably be enough to mirror along the nearest edge)
3. I calculate the Delaunay triangulation
4. I filter the segments that actually connect the original points (i.e. the ones inside the rectangle)
5. I take the averages the get the mean distance to neighbors defines by the Voronoi

Comments:
- Assuming an rectangular domain, by this procedure I enforce Voronoi edges along the rectangle without changing the Voronoi inside the rectangle (one would have to proof this)
- I attached two pictures



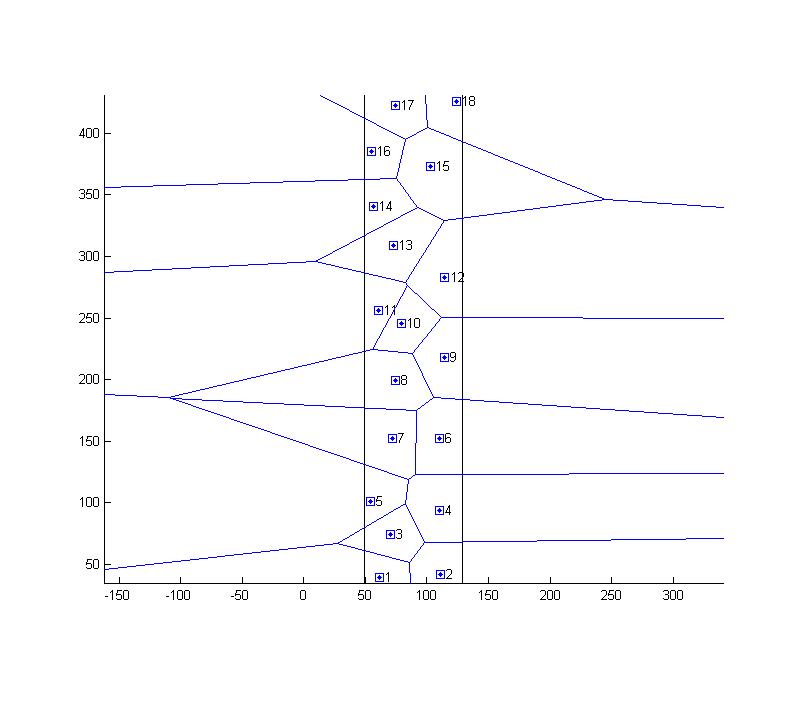
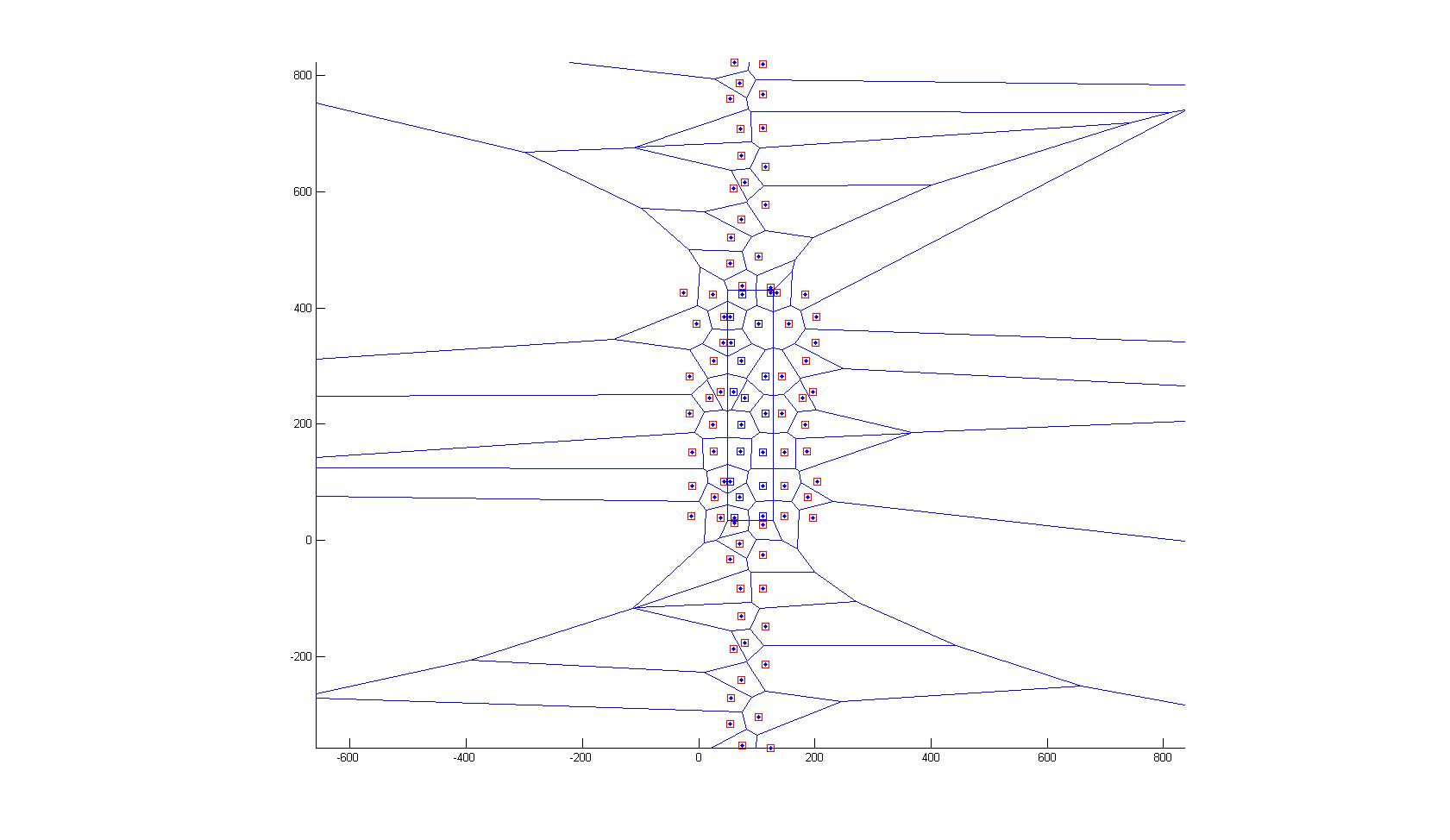
Due to my lack of imageJ programing skills I implemented in in Matlab.

If I come up with a better solution (and I am sure it exists), I'll post it.
Many regards,
Angelika